COGNITIVE NETWORK
-----------------
In "Linguistic Inversion" we have defined the founding structure of
RD Logic illustrated by Figure "Foundation of Logic". This structure
represents static support of deductive and inductive inferencing.
In order to support them dynamically it has to be completed with
Logical Operators. We shall introduce this complete, dynamic
inferencing structure (the "Cognitive Network" or "CN") with help
of a simple example "diagnostics",
In medical context we may talk about diseases encompassing Syndroms
which in turn encompass symptoms. We shall use "diagnosis" rather
than "disease" to make our example more general, pointing to all
sorts of AI applications detecting defects and failures.
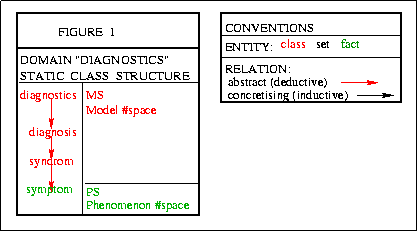
Fig. 1 is a graphic representation of Step 1 of defining the AI
Application, the general, static, deductive Class Structure:
"diagnostics" encompasses
("diagnosis" encompasses
("syndrom" encompasses
("symptom")))
Let's note that Abstract Classes marked in red and Factual Class
marked in green represent respectively the Model "space and the
Phenomenon #space defined in "Structure of Scientific Theories".
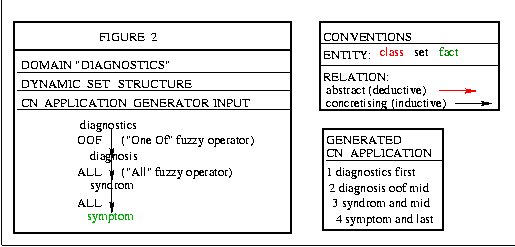
Fig. 2 illustrates Step 2, the dynamic, inductive Set Structure:
Step 2 particularities:
2.1.Concretisation. Deductive Factual Class of Step 1, is
interpreted inductively (Bottom Up) and concretised into Set
of Symptoms.
Following the concretising rule, Set-Parts concretise their
deductive Class Relations into concrete inductive Set Relations.
Via concrete Relations Aggregates are in turn concretised from
Classes into Sets. The process is recursive, so that all Entities
and Relations of our simple Hierarchy become concrete Sets and Set
Relations. (See Part "Foundations of Mathematics", Ch. "RD Construct
Theory").
In the general case of a Network structure not all Aggregates would
be concretised, but only those encompassing recursively the Facts.
(See "Reflection Spiral", Fig.2, Symbolic Structure 1, inductive).
2.2.Inferencing. Concrete Set Relations get associated with Logical
Operators. Fuzzy Inferencing and Fuzzy Logical Operators compose a
rather complex domain which is discussed in detail in the chapter
"Artificial Intelligence". Here we shall recall from "Exact nD
Propositional Calculus" that:
Dimensionality is local and for each Aggregate is determined by
the number of its Parts. This unlimited dimensionality requests
Operators capable to operate on any number of premises (Parts).
Now, some Operators map one to one from the 2D to the nD Calculus,
but other fork to more than one in nD, which introduces an
additional complication. Such is the case of "orr" (exclusive or)
which maps to nD as n distinct Operators, in 3D to "one-of",
"two-of" and "not-all". (Details in "Exact nD Propositional
Calculus").
Our example uses two Fuzzy Operators:
-"AND", as a syndrom encompasses all symptoms and a diagnosis
encompasses all syndroms,
-"OOF" (One Of), as only one of diagnosis may be chosen as base for
subsequent therapy.
2.3.Inferencing operates not on general Sets, but on particular Set
Instances. In Step 2 we define general inferencing Rules (in form
of Operators associated with Relations), which will be applied to
Set Instances in the subsequent Step 3.
2.3.Generating. Figure 2 contains enough information to become input
for automatically generating "Diagnostics" Application.
The Generator may be programmed to directly accept the graphic diagram
as input (the case of our prototype AI Application), or may be prompt
driven with the diagram supporting answers to prompts.
Fig. "Generated Cn Application" shows printout of "Diagnostics"
Application Schema generated with direct Graphic input. By "Schema"
we understand an executable Program comprising Containers' structure
corresponding to the Set structure, initially empty and open to be
filled with subsequently inputted Instances.
Fig. 3 illustrates Step 3, the inductive, inferencing,
Instance Structure.
This structure provides a theoretical illustration of the Application
instance structure obtained by inputting the properly interrelated
instances of the Set Structure. The Application printout of the Instances
Structure in indented form is shown in Fig. 4.
It represents "Explosion" or "Extension" of "1 diagnostics", i.e.
a recursive structured enumeration of its instances. As it shows
recursively the whole structure, we call it "Deep Explosion".
Fig. 4. CN Application. Deep Explosion of "diagnostics".
--------------------------------------------------------
1 diagnostics first
2 diagnosis_1_3 oof mid
3 syndrom_1_acf and mid
4 symptom_a and last
4 symptom_c and last
4 symptom_f and last
3 syndrom_3_bgh and mid
4 symptom_b and last
4 symptom_g and last
4 symptom_h and last
2 diagnosis_2_4 oof mid
3 syndrom_2_bcd and mid
4 symptom_b and last
4 symptom_c and last
4 symptom_d and last
3 syndrom_4_aeg and mid
4 symptom_a and last
4 symptom_g and last
4 symptom_e and last
2 diagnosis_3_4 oof mid
3 syndrom_3_bgh and mid repetition
3 syndrom_4_aeg and mid repetition
Legend:
1.Numbers starting the lines are "levels" of the Structure. Entity of
level N encompasses directly Enities of level N+1: "1 diagnostics"
encompasses "2 diagnosis_1_3", "2 diagnosis_2_4", "2 diagnosis_3_4".
"3 syndrom_2_bcd" encompasses "4 symptom_b", "4 symptom_c",
"4 symptom_d".
2."oof", "and" are Operators associated with relation between Enities of
level N+1 and N: 1 syndrom_1_acf = and 2 symptom_a and 2 symptom_c and 2
symptom_f, or in Polish Notation:
1 syndrom_1_acf = and (2 symptom_a, 2 symptom_c, 2 symptom_f)
In Polish Notation:
1 diagnostics = oof(2 diagnosis_1_3, 2 diagnosis_2_4, 2 diagnosis_3_4)
(is one of them).
"first" denotes the top Entity which is a pure Aggregate, having only
Parts, but no Aggregates. In terms of "diagnostics" Model it is the
Axiom. We shall discuss it in more detail in "Artificial Intelligence".
"mid" denotes "middle" Entities having both Parts and Aggregates.
In terms of the Model they are Theorems.
"last" denotes bottom Entities which are pure Parts having Aggregates,
but no Parts. In terms of the Model they are Facts, or Phenomena of the
Phenomenal #space.
"repetition" denotes an Entity which has already appeared in the indented
Structure and whose Explosion is not repeated for conciseness sake.
Discussing the Fig. 1 above we have indicated that bottom Entities of CN
structure represent Facts or Observations of the Phenomenon #space as
defined in "Structure of Scientific Theories". In our example bottom
Entities are "symptoms", marked accordingly to CN conventions as "last".
Bottom Entities are Premises of Inductive Inferencing. Their Certainty
does not result from any inferencing procedure and can only be set by
some Observation procedures external to CN. In the case of our
"diagnostics", "symptoms" may be set by sensors of some technological
device such as a space craft, or by a physician who observes symptoms
of a patient, which are more or less typical, strong or in one word
"certain". Fig. 5 shows an example of a distribution of symptoms'
certainties inputted to CN and printed out.
Fig. 5. CN Application. Input of symptoms' Certainties.
-------------------------------------------------------
NOTE: All Certainties are expressed in percents.
symptom_a and 98 last
symptom_b and 95 last
symptom_c and 96 last
symptom_d and 25 last
symptom_e and 18 last
symptom_f and 97 last
symptom_g and 98 last
symptom_h and 94 last
Starting from those premises CN executes the Inductive, bottom up
Inferencing whose results are shown in Fig. 6. It's the same structure as
that of Fig. 4 with added evaluated Certainty values.
Fig. 6. CN Application. Deep Explosion of evaluated Instances.
--------------------------------------------------------------
1 diagnostics 74 first
2 diagnosis_1_3 oof 80 mid
3 syndrom_1_acf and 93 mid
4 symptom_a and 98 last
4 symptom_c and 96 last
4 symptom_f and 97 last
3 syndrom_3_bgh and 89 mid
4 symptom_b and 95 last
4 symptom_g and 98 last
4 symptom_h and 94 last
2 diagnosis_2_4 oof 1 mid
3 syndrom_2_bcd and 18 mid
4 symptom_b and 95 last
4 symptom_c and 96 last
4 symptom_d and 25 last
3 syndrom_4_aeg and 12 mid
4 symptom_a and 98 last
4 symptom_g and 98 last
4 symptom_e and 18 last
2 diagnosis_3_4 oof 6 mid
3 syndrom_3_bgh and 89 mid repetition
3 syndrom_4_aeg and 12 mid repetition
Deep Explosion of the top Entity is in practical cases too long and too
complex to be grasped at a glance. Even our very small example may be
found not quite limpid. It is utile to navigate through the structure
with help of one level or "flat" explosion, as shown in Fig. 7-9.
Fig. 7. CN Application. Flat Explosion of the top Entity "diagnostics".
-----------------------------------------------------------------------
1 diagnostics 74 first
2 diagnosis_1_3 oof 80 mid
2 diagnosis_2_4 oof 1 mid
2 diagnosis_3_4 oof 6 mid
"diagnostics" encompasses "diagnosis_1_3", "diagnosis_2_4" and
"diagnosis_3_4" whose Certainties are respectively 80,1,6. The Inductive
Inferencing from the premises of Fig. 5 leads to the conclusion that
"diagnosis_1_3" is by far the most certain. The Certainty of choosing
"diagnosis_1_3" as one of ("oof") the three is evaluated in their
Aggregate "diagnostics" as 74.
Certainty of the top Entity "diagnostics" (74) qualifies as acceptable
the evaluation of the three mutually exclusive ("oof" Operator)
"diagnosis_..." and the implicitly suggested choice of "diagnosis_1_3".
Epistemological implication of the top Certainty and the determination of
"oof" algorithm will be discussed in "Artificial Intelligence".
Fig. 8. CN Application. Flat Explosions of the three "diagnosis".
-----------------------------------------------------------------
1 diagnosis_1_3 80 mid
2 syndrom_1_acf and 93 mid
2 syndrom_3_bgh and 89 mid
1 diagnosis_2_4 1 mid
2 syndrom_2_bcd and 18 mid
2 syndrom_4_aeg and 12 mid
1 diagnosis_3_4 6 mid
2 syndrom_3_bgh and 89 mid
2 syndrom_4_aeg and 12 mid
We note that and(93,89) = 80; and(18,12) = 1; and(89,12) = 6;
Detais of "and" algorithm will be discussed in "Artificial Intelligence".
Fig. 9. CN Application. Flat Explosions of "syndroms".
------------------------------------------------------
1 syndrom_1_acf 93 mid
2 symptom_a and 98 last
2 symptom_c and 96 last
2 symptom_f and 97 last
1 syndrom_2_bcd 18 mid
2 symptom_b and 95 last
2 symptom_c and 96 last
2 symptom_d and 25 last
1 syndrom_3_bgh 89 mid
2 symptom_b and 95 last
2 symptom_g and 98 last
2 symptom_h and 94 last
1 syndrom_4_aeg 12 mid
2 symptom_a and 98 last
2 symptom_g and 98 last
2 symptom_e and 18 last
Explosion structures show for an Aggregate (or Conclusion in logical
terms) the Parts it encompasses (or Premises), either directly
(Flat Explosion) or recursively, till the bottom of structure
(Deep Explosion).
One may be on the other hand interested for a Part (or Premise), by which
Aggregates it's encompassed (to which Conclusions it contributes)
directly (Flat Implosion) or recursively till the top of structure (Deep
Implosion). Fig. 10-11. show Flat and deep Implosion of "symptom_a".
Fig. 10. CN Application. Flat Implosion of "symptom_a".
-------------------------------------------------------
1 symptom_a 98 last
2 syndrom_1_acf and 93 mid
2 syndrom_4_aeg and 12 mid
Fig. 11. CN Application. Deep Implosion of "symptom_a".
-------------------------------------------------------
1 symptom_a 98 last
2 syndrom_1_acf and 93 mid
3 diagnosis_1_3 and 80 mid
4 diagnostics oof 74 first
2 syndrom_4_aeg and 12 mid
3 diagnosis_2_4 and 1 mid
4 diagnostics oof 74 first
3 diagnosis_3_4 and 6 mid
4 diagnostics oof 74 first